Plasmonic focus * Localized surface plasmon resonances * A brief compendium on small metal particles * Fine metallic nanoparticles * Decay rates * Surface scattering correction * Dynamic depolarization
On an alternative
The performance of individual metal nanoparticles (MNPs)
is crucially influenced by the localized surface plasmon resonance (LSPR)
homogeneous line width or, alternatively, the
LSPR dephasing time. So far, two main paths have been pursued in order to improve
over the performance of individual spherical metal nanoparticles MNPs: (1) various
core-shell MNP morphologies and (2) non-spherical MNP external shapes such as rods,
cubes, and prisms.
About a third alternative path read
here.
Elementary properties of localized surface plasmon resonances
(LSPR) of small metal (nano)particles
The field of small metal particles has been exploding in recent years,
with the ongoing development
resulting in many exciting applications in biology, energy conversion,
medicine, sensing, etc. At a first glance, basic theoretical
principles underlying the properties of localized surface plasmon resonances (LSPR)
should have been known and well understood by now. Remember
an excellent monograph by C. F. Bohren and D. R. Huffman,
Absorption and Scattering of Light by Small Particles
(John Wiley & Sons, New York, 1998). However,
even for a spherical particle, the small particle
limit is not as simple as it seems. The reason being that the respective
coefficients of the long wavelength expansion in terms of power series in the size parameter x=ka have eps+2 in denominator,
and thus become singular at the proximity of a
surface plasmon resonance. [See e.g. such an expansion for the Mie's coefficient
a_1 on p. 295 of R. Gans and H. Happel, Zur Optik kolloidaler Metallösungen,
Annalen der Physik IV. Folge 29, pp. 277-300 (1909), which is reproduced as Eq. (11)
in W. T. Doyle and A. Agarwal,
Optical extiction of metal spheres,
J. Opt. Soc. Am. 55, 305-308 (1965).]
The sections below are intended to highlight and summarize
some of the basic theoretical principles underlying the optical
properties of small metal particles in their applications involving a
modification of decay rates and scattering,
because, at times, some of the properties repeatedly continue
of having been rediscovered till nowdays.
Radiative reaction correction
An oscillating dipole loses its energy due to the radiation it emits.
As a result, the dipole oscillations are damped.
This radiation damping is described by the Abraham-Lorentz equation,
which can be found in any standard textbook on classical electrodynamics,
such as that by J. D. Jackson [see Sec. 16.2 and Eqs. (16.8-9) therein].
Such a radiation damping applies to any oscillating dipole, be it an elementary
molecular dipole or the dipole induced on a small (nano)particle.
Since the induced dipole moment of a small (nano)particle
is directly related to its polarizability,
such a radiation damping translates to that of a particle polarizability.
This point has been first emphasized as early as in 1982
by Wokaun, Gordon, and Liao [1] [see Eqs. (1) and (2) therein],
although, as referred to by Ohtaka and Inoue [3] [see Eq. (2.7) therein],
it was anticipated much earlier in the textbook
by Landau and Lifshitz [2].
Not aware of the above work, the necessity of the radiative reaction
term in the polarizability has been rediscovered 6 years later
by B. T. Draine [4]
within the coupled dipole approximation (CDA).
Theoretically, the radiation damping term is necessary for
the extinction cross section to be the
sum of the scattering and absorption cross sections, which is sometime
misleadingly referred to as unitarity
in the dipole approximation (see also Appendix C of [5]).
References:
- A. Wokaun, J. P. Gordon, and P. F. Liao,
Radiation Damping in Surface-Enhanced Raman Scattering,
Phys. Rev. Lett. 48, 957-960 (1982) (published 5 April 1982).
- L. D. Landau and E. M. Lifshitz,
The Classical Theory of Fields (Oxford, Pergamon, 1959)
p 186.
- K. Ohtaka and M. Inoue,
Electromagnetic aspects of the enhanced Raman scattering by a
molecule adsorbed on a polarisable sphere,
J. Phys. C: Solid State Phys. 15 6463-6480 (1982) (received 21 May 1982).
- B. T. Draine,
The discrete-dipole approximation and its application to
interstellar graphite grains,
Astrophys. J. 333, 848-872 (1988).
- A. Moroz, Depolarization field of spheroidal particles,
J. Opt. Soc. Am. B 26(3), 517-527 (2009) [pdf].
Belongs to the most-downloaded publications of J. Opt. Soc. Am. B in the field of
plasmonics.
(Shows that the hypothesis of a uniform polarization within
a spheroidal particle is incompatible with the exact limit of polarizability
in the small particle limit up to the order x**2 when the size parameter x--> 0.
Accompanying F77 code sphrd.f to determine extinction efficiency
in various long-wavelength approximations discussed in the article.
See here for on-line supplementary material.
See also my worksheet involving some intermediary calculations.)
Dynamic depolarization
As observed by Meier and Wokaun [1],
starting from the electrostatic solution at
the value of size parameter x=ka=0,
the maximum electric field intensity enhancement at the surface
of a sphere
is seen first to increase with sphere radius a.
At a=12.5 nm, the intensity enhancement is
7.8% larger than the electrostatic limit.
A closer examination reveals
that, for silver, this maximum occurs at lambda = 357 nm,
which is slightly longer than the electrostatic value, lambda =355 nm.
For larger particles the enhancement strongly decreases; it shifts to
longer wavelengths and is broadened.
A second maximum at shorter wavelength is seen at a>30 nm.
From the monograph by Bohren&Huffman [see Eq. (12.13) in Sec. 12.1.1],
the surface plasmon position of a spherical particle shows
the following size dependence:
epsilon_r = - [2 + (12/5) x**2] epsilon_h
(R1)
where epsilon_r is the
dielectric constant of a sphere at the resonance position
and epsilon_h is the
dielectric constant of the surrounding medium.
The above size dependences cannot be accounted for by
a polarizability comprising only the k**3-dependent
radiative reaction term. One needs in addition
a k**2-dependent dynamic depolarization term [1,3].
All the terms in the electron dipole polarizability are included
if the electron dipole polarizability is
determined directly from the dipole T-matrix element on using
the relation
alpha = -i (6*pi/k**3) T = -i (3/2*k**3) T,
(R2)
where the first (second) expression holds in the SI (gauss) units.
(A free T-matrix code for metallic particles is available in Ref.
[4] herein below.)
As shown by Dungey and Bohren [5],
the use of such a polarizability brings a significant improvement
within the coupled/discrete dipole approximation (CDA/DDA)
over the schemes incorporating only the radiative reaction term.
It is worth of reminding here that the static sphere polarizability
alpha = a**3 * (epsilon-epsilon_h)/(epsilon+2*epsilon_h),
which is the Rayleigh (x ---> 0) limit
of the expression (R2),
is not unitary (see also Appendix C of [6])
and is insufficient in describing essential features of small
metal naparticles, such as the size-dependence of a red-shift
of the surface plasmon resonance (SPR) (see Eq. (R1) and Sec. 12.1.1. of [2])
The Meier and Wokaun recipe [1] is based upon
two hypothesis. The first hypothesis is
that the polarization
is homogeneous over the volume of the particle.
The second hypothesis, which can be viewed as
a continuation of the first one, is
that the same dipole moment is assigned to each volume
element of the particle.
Given the above two hypothesis,
Ref. [6] provides an exact solution for the case
of a spheroid and, in doing so, it also amends the original
Meier and Wokaun result for a sphere [1].
In Ref. [6], the dynamic k**2-dependent
depolarization component of E_d
has been shown to depend on dynamic geometrical factors,
which can be expressed in terms of the standard
geometrical factors of electrostatics.
The Meier and Wokaun recipe itself was shown to be equivalent
to a long-wavelength limit of the Green's function technique.
The resulting Meier and Wokaun long-wavelength
approximation (MWLWA) exhibits a red-shift
compared against exact T-matrix results.
The red-shift is a hallmark of the Meier and Wokaun long-wavelength
approximation: it will persist unless the assumption
of a uniform field
E_i inside a particle is relaxed [6].
For a sphere it is possible to get rid
of the red-shift by assuming rather simple form
of a weak nonuniformity of the field
E_i inside a particle that can be fully
accounted for by a renormalization of the dynamic
geometrical factors [6].
Interestingly enough, for electric field oriented along the spheroid rotational axis,
the work by Kuwata et al [7] has anticipated
dynamic depolarization factors by purely empirical formula
obtained by best fit to numerical results, in which case
dynamic depolarization factors were fitted by a polynom
of the 3rd order in the standard
geometrical factor of electrostatics L_z. In contrast,
analytic results of Ref. [6] suggest that a linear L_z dependence,
but with eccentricity-dependent coefficients, may be enough.
The long-wavelength approximations of Refs. [6,7] accurately match
the SPR position, height, and linewidth
of the exact results for noble particles with an
equivalent-volume-sphere radius of up to 50 nm in the visible.
Note in passing that the linewidth Gamma directly determines
the plasmon dephasing time T_2=2 hbar/Gamma,
where hbar is the Planck constant,
the quality factor Q of the resonance at the SPR frequency omega_r
via the formula Q = omega_r/Gamma,
and the local field enhancement factor |f|
(in a harmonic model |f| = Q).
Recently, the results of Ref. [6]
have been extended to provide an
approximation for the polarizability for large metallic
spheroidal nanoshells [8].
References:
- M. Meier and A. Wokaun,
Enhanced fields on large metal particles: dynamic
depolarization,
Opt. Lett. 8, 581-583 (1983).
- C. F. Bohren and D. R. Huffman, Absorption and
Scattering of Light by Small Particles
(John Wiley & Sons, New York, 1998).
- M. Kerker, D.-S. Wang, and H. Chew,
Surface enhanced Raman scattering (SERS) by molecules adsorbed
at spherical particles: errata,
Appl. Opt. 19, 4159-4174 (1980).
- A. Moroz, Improvement of Mishchenko's T-matrix code for absorbing
particles,
Appl. Opt. 44(17), 3604-3609 (2005). [pdf]
(Accompanying F77 code is available here together with
routines zger.f and zsur.f;
see also routines zge.f and zsu.f
for multiplication from the other side.)
- C. E. Dungey and C. F. Bohren,
Light scattering by nonspherical particles: a refinement
to the coupled-dipole method,
JOSA A 8, 81-87 (1991).
- A. Moroz, Depolarization field of spheroidal particles,
J. Opt. Soc. Am. B 26(3), 517-527 (2009).
(Accompanying F77 code sphrd.f to determine extinction efficiency
in various long-wavelength approximations discussed in the article.
See here for on-line supplementary material.
)
- H. Kuwata, H. Tamaru, K. Esumi, and K. Miyano,
Resonant light scattering from metal nanoparticles:
Practical analysis beyond Rayleigh approximation,
Appl. Phys. Lett. 83(22), 4625-4627 (2003).
-
H. Y. Chung, P. T. Leung, and D. P. Tsai,
Dynamic modifications of polarizability for large metallic
spheroidal nanoshells,
J. Chem. Phys. 131, 124122 (2009).
Surface scattering corrections to the dielectric function of nanoparticles
The dielectric constant of a small metallic particle is dependent
on the size and shape of the particle via lowering of the effective
mean free path L of conduction electrons due to collisons of the
conduction electrons with the particle surface (the free-path effect),
resulting in the so-called
size-corrected dielectric function.
Indeed, the damping constant in the Drude theory is the inverse
of the collision time of the conduction electrons, and the latter
decreases because of additional collisions with the boundary of the particle.
Obviously, this dependence is
important, when the particle size is smaller than the conduction electron
mean free path (52 nm for silver [1,3], 42 nm for gold [2],
and 45 nm for Cu [3]).
The free-path effect can be incorporated in the dielectric constant
of free-electron metals
according to the recipe by Kreibig and Fragstein [1].
Although the effect of the mean free path limitation on the real part of the
dielectric function is slight, the effect on the imaginary part is often
substantial. For instance, for small silver particles near a SPR,
the imaginary part is enhanced by more than 10% for particles of radius 100 nm,
whereas the imaginary part is twice the bulk value for the radius of about 11.5 nm.
The effect of the decreased mean free path is to increase the width and lower
the peak height of the surface plasmon absorption (see Sec. 12.1.6 of
Bohren&Huffman [4]).
For a homogeneous sphere of a radius R,
essentially two different classical surface scattering
models were proposed: (i) diffusive and (ii) isotropic
scattering models.
-
Euler diffusive surface scattering model [5] is
the oldest one. The model is
concerned with the trajectories immediately after
individual scattering events.
The electron reflexion on
the boundary surface is taken to be fully isotropic, meaning there is equal
probability for electron to be scattered at any angle with respect
to the surface inward normal.
-
Isotropic scattering is, in contrast to the Euler model [5],
concerned with
the trajectories immediately before scattering events.
No explicit assumption is made about
individual scattering events at the enclosure boundary
except that the scattering events conspire to maintain
a homogeneous and isotropic particle distribution in the electron
enclosure [6].
Independently of the above scattering models,
researches working in the field of ergodic billiards have also
figured out a mean free path in a classical ergodic billiard.
-
Billiard scattering model [7,8] presumes a specular reflection
at the enclosure boundary, i.e., the angle of incidence equals the angle of reflection.
This allows one to unambiguously follow any given electron trajectory.
In contrast to previous models, further considerations in the billiard case
follow in the phase space on using the concept of invariant
probability measures. The billiard measure comprises an
extra cos(theta)-factor with regard to the Euler measure,
where theta is the polar angle measured with regard to the inward normal
at the particle surface.
For a homogeneous sphere of radius R one obtains
L = R in the diffusive case and L = 4R/3
in the isotropic and billiard cases. The latter results has also
been recovered by Coronado and Schatz within a
geometrical probability approach [9].
In Ref. [10], the mean free path
for a spherical shell geometry was calculated
(i) on assuming Euler diffusive surface scattering
and (ii) under the assumption of a homogeneous and isotropic electron
distribution within a shell.
Further, the general billiard formula of Refs. [7,8]
was confirmed in the nanoshell case by an explicit
averaging procedure.
The extra cos(theta)-factor in the billiard measure
has been interpreted as that the (electron) enclosure surface is a
Lambertian surface.
The latter is distinguished by a fact that the radiant intensity observed from it
is directly proportional to the cosine of the angle theta between
the observer's line of sight and the surface normal, and hence
when an area element on the surface is viewed from any angle,
it has the same radiance. (An example a perfect Lambertian radiator is a black body, and,
to a large extent, the Sun in the visible spectrum.) Consequently,
the billiard measure can be interpreted as that the electron scattering
events on the domain surface conspire to produce
a diffusive Lambertian surface.
The condition of specular reflections can then be abandoned.
Let D be the shell thickness and
R the outer shell radius.
Preliminary experimental results,
which were performed exclusively within the range D/R < 0.25
and which shown a linear dependence of L on D,
are compatible with
the billiard, or Lambertian, scattering model and rule out
both the Euler diffusive scattering and the isotropic scattering.
The billiard model characterized by the Lambertian scattering on
the electron enclosure surface is distinguished by the following properties
in the nanoshell case [10]:
-
It is the only model which yields a linear
behavior of the mean free path L
on the shell thickness D in the thin shell limit
(up to D/R approx 0.3).
Compare that with
L_d ~ (D/2) ln (R/D) in the diffusive case, and with
L_i ~ 14(2RD)**(1/2)/[3 ln (R/D)] in the isotropic case.
- For any shape of a bounded and connected electron enclosure
and in any space dimension,
the surface scattering mean free path L is straightforwardly
determined by substituting the surface
S and volume V of the enclosure into the general
billiard formula [7,8,10], which in 3D reduces to
L = 4*V/S,
(C1)
and in 2D reduces to
L = pi* V/S.
(C2)
-
The billiard measure is the only measure which yields
a finite result when
the integral for the slab geometry is performed.
It goes without saying that the result coincides
with the thin-shell limit in the spherical shell geometry [10].
- On using the
Birkhoff-Khinchin theorem, the billiard mean free path can be interpreted
as the time average of the free paths along
typical trajectories [7,8].
- Gives the best agreement
with the experimental data and agrees with the experimental findings
of Ref. [11] without any fitting parameter.
- Appears to agree with quantum-mechanical calculations.
The success of the Euler diffusive scattering model in the homogeneous sphere
case seems to be purely accidental, since all the classical scattering models
yield a linear dependence of the mean free path on the sphere
radius with minor differences in the slope.
Contrary to homogeneous sphere case, the mean free path in the shell geometry
turns out to be much more sensitive to underlying model assumptions of electron
surface scattering.
Consequently, future experiments on single and well-controlled
dielectric core-metal shell nanoparticles can much easier
differentiate in between competing models of surface scattering.
This would enable one to assess more precisely
the contribution of other mechanisms, such as chemical interface
damping [12], to overall plasmon resonance damping.
Quite amazingly, although Lermé et al [13] did not emphasize it,
their experimental data regarding
silver nanospheres fit nicely to the billiard model [10].
The latter yields for the mean-free path the value of 4R/3
(e.g. eq. 141 of Ref. [10]) which,
when compared with eq 1 of [13], would have yielded g=3/4=0.75.
The latter value is almost in the middle of an
overall experimental value of
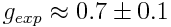 determined by Lermé et al [13].
Compared to the billiard model, the diffusive
model of Euler and Kreibig would yield for the
mean-free path the value of R, or g=1 [10].
determined by Lermé et al [13].
Compared to the billiard model, the diffusive
model of Euler and Kreibig would yield for the
mean-free path the value of R, or g=1 [10].
As suggested to me by Professor C. F. Bohren, the history of the
above Eqs. (C1) and (C2) goes much further and derives
from early results by Cauchy, who studied the
average projected area 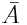 of convex bodies [14,15].
The relevant Cauchy theorem states that in three spatial dimensions [14,15]
of convex bodies [14,15].
The relevant Cauchy theorem states that in three spatial dimensions [14,15]
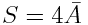 (C3)
(C3)
where S is the corresponding surface area of a convex body.
The average is taken over all possible orientations in space.
Other way round, the average projection
of a convex body onto a plane is equal to one quarter of its surface area.
In reactor and in other branches of physics the mean-free path
of a single particle bouncing off the walls of a convex body
has been then heuristically determined as [16-19]
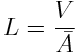 (C4)
(C4)
One can verify that on substituting for 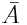 from (C3) into (C4) one recovers (C1).
This relation has also been used in the derivation of the
Sabine equation in acoustics, using a geometrical
approximation of sound propagation.
from (C3) into (C4) one recovers (C1).
This relation has also been used in the derivation of the
Sabine equation in acoustics, using a geometrical
approximation of sound propagation.
In two dimensions, the
average projected area 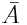 of a convex body reduces to an average projected length [20]
of a convex body reduces to an average projected length [20]
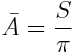 (C5)
(C5)
The average chord length is thus, with V the area of the figure
and S the circumference of the figure,
given by
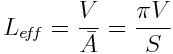 (C6)
(C6)
which is identical to (C2).
However, a core-shell problem
becomes the problem of calculating the mean-free path in a
circular shell region
that is (i) neither convex nor (ii) simply connected.
This means that the early results
by Cauchy [14,15], Czuber [16],
Dirac [17], Weinberg and Wigner [18], and others [9,18-20],
which yield the mean free path in terms of
the geometrical parameters of a convex domain,
can no be longer applied. Nevertheless, the validity
of the geometric formula (C6) can still be established
in the case of the billiard scattering [21].
In analogy with the 3D case [10], a different result is then obtained
in the diffusive case
[21].
References:
- U. Kreibig,
Electronic properties of small silver particles: the optical constants and
their temperature dependence,
J. Phys. F: Met. Phys. 4, 999-1014 (1974).
- U. Kreibig and C. V. Fragstein,
The limitation of electron mean free path in small silver particles,
Z. Physik A 224(4), 307-323 (1969).
- F. W. Reynolds and G. R. Stilwell,
Mean Free Paths of Electrons in Evaporated Metal Films,
Phys. Rev. 88, 418-419 (1952).
- C. F. Bohren and D. R. Huffman, Absorption and
Scattering of Light by Small Particles
(John Wiley & Sons, New York, 1998).
- J. Euler, Infrared properties of metals and the mean free paths of conduction
electrons,
Z. Phys. 137, 318-332 (1954).
- U. Kreibig,
Small silver particles in photosensitive glass: Their nucleation and growth,
Appl. Phys. 10(3), 255-264 (1976).
-
N. Chernov, Entropy, Lyapunov Exponents and Mean Free Path for Billiards,
J. Stat. Phys. 88(1-2), 1-29 (1997).
[ps]
- N. Chernov and R. Markarian, on-line book
Introduction
to the Ergodic Theory of Chaotic Billiards.
- E. A. Coronado and G. C. Schatz,
Surface plasmon broadening for arbitrary shape nanoparticles:
A geometrical probability approach,
J. Chem. Phys. 119(7), 3926-3934 (2003).
- A. Moroz, Electron mean-free path in a spherical shell geometry,
J. Phys. Chem. C 112(29), 10641-10652 (2008).
(The article has been supplemented with a detailed
Electronic Supporting Information. See also an accompanying F77 code fsc.f to calculate the mean-free path
for various model cases discussed in the article.)
- G. Raschke, S. Brogl, A. S. Susha, A. L. Rogach, T. A. Klar,
J. Feldmann, B. Fieres, N. Petkov, T. Bein, A. Nichtl, and K. Kürzinger,
Gold Nanoshells Improve Single Nanoparticle Molecular Sensors,
Nano Lett. 4(10), 1853-1857 (2004).
- H. Hövel, S. Fritz, A. Hilger, U. Kreibig, and M. Vollmer,
Width of cluster plasmon resonances: Bulk dielectric functions
and chemical interface damping,
Phys. Rev. B 48, 18178-18188 (1993)
[pdf].
-
J. Lermé, H. Baida, C. Bonnet, M. Broyer,
E. Cottancin, A. Crut, P. Maioli, N. Del Fatti,
F. Valle, and M. Pellarin,
Size Dependence of the Surface Plasmon Resonance
Damping in Metal Nanospheres,
J. Phys. Chem. Lett. 1(19), 2922-2928 (2010).
-
A. Cauchy, Memoire sur la rectification des courbes
et la quadrature des surfaces courbes
(Paris, 1832). Reproduced in
Oevres Complčtes, 1st series, Vol. 2, p. 167
(Gauthiers Villars, Paris 1908).
-
A. Cauchy, C. R. Acad. Sci., Paris, 13, 1060 (1841).
A short account of his results [14] in the
form of theorems was later published in the Comptes rendus,
but no formal proof was given.
-
E. Czuber,
Zur Theorie der geometrischen Wahrscheinlichkeiten,
Sitzungsberichte der mathematisch-naturwissenschaftliche
Klasse der Kaiserlichen Akademie der Wissenschaften
Wien 90(2), 719-742 (1884).
-
P. A. M. Dirac,
Approximate rate of neutron multiplication for
a solid of arbitrary shape and uniform density,
British Report MS-D-5, Part I, 1943.
-
V. Vouk,
Projected area of convex bodies,
Nature 162, 330-331 (1948).
-
A. M. Weinberg and E. P. Wigner,
The Physical Theory of Neutron Chain Reactors,
(The University of Chicago Press, Chicago, 1958).
-
W. J. M. de Kruijf and J. L. Kloosterman,
On the average chord length in reactor physics,
Ann. Nucl. Energy 30(5), 549-553 (2003).
- A. Moroz, Electron mean-free path in metal coated
nanowires,
J. Opt. Soc. Am. B 28(5), 1130-1138 (2011).
(The article has been supplemented with a detailed
Supporting Information. See also an accompanying F77 code
fsc2d.f to calculate the mean-free path for various model cases discussed in the article.)
Decay rates of atoms and molecules in a proximity of small (nano)particles
Although Pol and Bremmer [1,2] and Fock [3]
treated the problem of diffraction of electromagnetic waves radiating from a
point source outside an absorbing sphere as early as in 1937 and 1946, respectively,
eventual application to the problem of atomic dipoles interacting with
small micro- and nano-particles followed much later with the work by
Ruppin [4] and Chew [5,6].
Kim et al [7] then worked out
a comprehensive treatment of the classical decay rates for a molecule
in the vicinity of a spherical surface through the
application of the work of Pol and Bremmer [1,2] and
that of Fock [3].
This theory took full advantage of the Hertz vector formalism,
which was claimed to be mathematically simpler than
the Lorenz-Mie approach, which uses the vector harmonic
expansions. Results were
obtained for both radiative and nonradiative transfer when the molecule
is located outside or inside the surface.
All the above results were tailored for homogeneous particles.
I'm proud
to provide in my articles [8,9] an extension for
the classical electromagnetics problem of
a dipole radiating inside and outside a stratified sphere
consisting of an arbitrary number of concentric spherical shells.
There is no limitation on the dipole position,
the number of the concentric shells, the shell medium, nor on
the sphere radius. Electromagnetic fields were
determined anywhere in the space, the time-averaged
angular distribution of the radiated power, the total radiated power,
Ohmic losses due to an absorbing shell, and Green's function
were calculated.
The results were applied to inelastic
light scattering (fluorescence and Raman), the radiative and nonradiative
normalized decay rates, and frequency shift. Using correspondence principle,
the radiative decay rate
was calculated from the Poynting vector, whereas the nonradiative
decay rate was calculated from the Ohmic
losses inside a sphere absorptive shell.
Fast and numerically stable transfer-matrix solution
has been incorporated into the respective F77 codes CHEW and CHEWFS, which are
freely available here and
here,
respectively.
In Ref. [9] frequency shifts, radiative decay rates,
the Ohmic loss contribution to the nonradiative decay rates,
fluorescence yield, and photobleaching of
a two-level atom radiating anywhere inside or outside
a complex spherical nanoshell with a dielectric core and three
alternating gold and silica concentric spherical shells were determined. An
application of the above codes for a homogeneous metal
nanoparticle can be found in Ref. [10].
Coincidentally, one of the core-shell particle geometries
studied in my article [8] correspond to that of a recently
reported spaser-based nanolaser [11].
References:
- B. van der Pol and H. Bremmer,
Diffraction of electromagnetic waves from an electrical point source
round a finitely conducting sphere, with applications to radio
telegraphy and the theory of the rainbow I,
Phil. Mag. 24, 141-176 (1937).
(The very first calculations of radiative decay rates
for vertical (radial) dipole).
-
B. van der Pol and H. Bremmer,
Diffraction of electromagnetic waves from an electrical point source
round a finitely conducting sphere, with application to radio
telegraphy and theory of the rainbow. II,
Phil. Mag. 24, 825-864 (1937).
(The very first calculations of radiative decay rates
for vertical (radial) dipole).
-
V. A. Fock,
The fields of a vertical and horizontal dipole above the earth surface,
Soviet. Phys. JETP 19, 916-929 (1946).
(The very first calculations of radiative decay rates for
horizontal (tangential) dipole).
-
R. Ruppin,
Decay of an excited molecule near a small metal sphere,
J. Chem. Phys. 76, 1681-1684 (1982).
- H. Chew,
Transition rates of atoms near spherical surfaces,
J. Chem. Phys. 87, 1355-1360 (1987).
We study the transition rates of atoms
inside and outside dielectric spheres
- H. Chew, Radiation and lifetimes of atoms inside dielectric
particles,
Phys. Rev. A 38, 3410-3416 (1988).
-
Y. S. Kim, P. T. Leung, and T. F. George,
Classical decay rates for molecules in the
presence of a spherical surface: A complete treatment,
Surf. Sci. 195, 1-14 (1988).
- A. Moroz, A recursive transfer-matrix solution for a dipole radiating inside and
outside a stratified sphere,
Ann.
Phys. (NY) 315(2), 352-418 (2005). (published online on 7 October 2004)
[story behind this article]
(accompanying F77 code CHEW and limited MS Windows
executable)
- A. Moroz, Spectroscopic properties of a two-level atom interacting with a complex
spherical nanoshell,
Chem. Phys. 317(1), 1-15 (2005).
(published online on 9 August 2005) [quant-ph/0412094]
(see its on-line Appendix A for a MS Windows executable;
source F77 code CHEWFS)
- A. Moroz, Non-radiative decay of a dipole emitter close to a metallic nanoparticle: Importance of higher-order multipole contributions,
Opt. Commun. 283(10), 2277-2287 (2010).
[arXiv:0909.4878]
(accompanying F77 code CRMNT and limited MS Windows
executable)
- M. A. Noginov, G. Zhu, A. M. Belgrave, R. Bakker, V. M. Shalaev,
E. E. Narimanov, S. Stout, E. Herz, T. Suteewong, and U. Wiesner,
Demonstration of a spaser-based nanolaser,
Nature 460, 1110-1112 (2009).
Multilayered nanoshells
Recently, Alu and Engheta [1] have brought
multilayered plasmonic shells into the spotlight
as a model system for optical invisibility cloak.
However, when dealing with dispersive and absorbing shells,
one has to take into account not only
surface scattering corrections to the dielectric function
(btw., there is no discussion of this
point in Ref. [1]) but also another subtle feature:
In the case of an absorbing shell
it may happen that the linearly independent spherical Bessel functions
j_l and y_l (see Sec. 10 of Ref. [2] for
notations) are in fact related in finite mathematics by
y_l approx i*j_l
(R3)
up to almost all significant digits in double precision!!!
This pathological behaviour can easily be demonstrated on the example
of j_0 and y_0.
Recall that j_0=(e^{iz}-e^{-iz})/(2iz) and
y_0=-(e^{iz}+e^{-iz})/(2z).
Thus, for sufficiently large Im z >0, each of j_0 and y_0
would be dominated by the e^{-iz}/(2z) term, resulting
in j_0 ~ i e^{-iz}/(2z) and y_0 ~ - e^{-iz}/(2z)
that implies the above relation (R3).
Consequently, if the spherical Hankel functions h_l
of the first kind are formed as the sum [2]
h_l = j_l + i*y_l,
their precision may be drastically compromised.
Indeed, the above relation would then for Im z >> 1
determine a much smaller
number (recall h_0=-ie^{iz}/z << 1) from the
sum of two much bigger numbers (recall j_0 ~ i e^{-iz}/(2z) >> 1
and y_0 ~ - e^{-iz}/(2z) >> 1).
Therefore, it is always recommended
to determine h_l by a direct independent recurrence,
such as that proposed by
Mackowski et al [3] [see recurrences (63),(64) therein].
Otherwise (see Sec. 4.6 and model calculations
for a nanoshell C in Ref. [4]) the radiative decay for
the interior of a nanoshell may differ by up to four-orders of magnitude
from the correct one.
If one can perform calculations in an extended precision,
this pathological behaviour can be largely overcome, yet the independent
recurrence by Mackowski et al [3] is still highly recommended.
References:
- A. Alu and N. Engheta,
Multifrequency optical iInvisibility cloak with layered plasmonic shells,
Phys. Rev. Lett. 100, 113901 (2008).
-
M. Abramowitz and I. A. Stegun,
Handbook of Mathematical Functions
(Dover Publications, New York, 1973)
- D. W. Mackowski, R. A. Altenkirch, and M. P. Menguc,
Internal absorption cross sections in a stratified sphere,
Appl. Opt. 29(10), 1551-1559 (1990).
- A. Moroz, Spectroscopic properties of a two-level atom interacting with a complex
spherical nanoshell,
Chem. Phys. 317(1), 1-15 (2005).
(published online on 9 August 2005)
[quant-ph/0412094]
(see its on-line Appendix A for a MS Windows executable;
source F77 code CHEWFS)
[
Refreshing some of plasmonic headlines
]
[
A Drude model fit parameters to the dielectric function
of free electron metals
]
[
Negative refractive index material
headlines long before Veselago work and going back as far as to 1904...
]
[
Permanently free focus issue on 'Plasmonics', edited by
Sergey Bozhevolnyi and Francisco Garcia-Vidal in New Journal of Physics
]
[
Selected Links on Photonics,
Photonic Crystals, Numerical Codes, Free Software
]
[
Some photonic crystal headlines,
at least 25 years old ...
|
An Early History of
Acoustic and Photonic Crystals
]
[
Main page
|
My personal webpage
|
Full list of my scientific publications
|
My most frequently cited articles
]
© Alexander Moroz,
January 2, 2009 (last updated January 19, 2012)
![]() determined by Lermé et al [13].
Compared to the billiard model, the diffusive
model of Euler and Kreibig would yield for the
mean-free path the value of R, or g=1 [10].
determined by Lermé et al [13].
Compared to the billiard model, the diffusive
model of Euler and Kreibig would yield for the
mean-free path the value of R, or g=1 [10].
![]() of convex bodies [14,15].
The relevant Cauchy theorem states that in three spatial dimensions [14,15]
of convex bodies [14,15].
The relevant Cauchy theorem states that in three spatial dimensions [14,15]
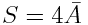 (C3)
(C3)
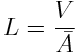 (C4)
(C4)
![]() from (C3) into (C4) one recovers (C1).
This relation has also been used in the derivation of the
Sabine equation in acoustics, using a geometrical
approximation of sound propagation.
from (C3) into (C4) one recovers (C1).
This relation has also been used in the derivation of the
Sabine equation in acoustics, using a geometrical
approximation of sound propagation.
![]() of a convex body reduces to an average projected length [20]
of a convex body reduces to an average projected length [20]
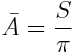 (C5)
(C5)
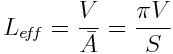 (C6)
(C6)